tsujimotterの下書きノート

このブログは「tsujimotterのノートブック」の下書きです。数学の勉強過程や日々思ったことなどをゆるーくメモしていきます。下書きなので適当です。

記事一覧はこちらです。このブログの趣旨はこちら。

メインブログである「tsujimotterのノートブログ」はこちら。

朝岩澤理論５：岩澤理論とその展望（上）

朝岩澤理論

tsujimotter-sub.hatenablog.com

の第５週目。


ポイントをまとめていく。あくまで自分のメモ用です。

第５週目（2017/2/17 〜 2017/2/23）

2/17：イデアル類群の構造の補足（3.1.3）

  • 新しい節に入った。ここからしばらくは CM体 (Complex Multiplication field) のお話。
  • CM体：
    • (i) 総実代数体 K^+ の総虚な２次拡大
    • (ii)(a) J: \mathbb{C} \to \mathbb{C} を複素共役とするとき、埋め込み \tau: K \hookrightarrow \mathbb{C} に対して J_\tau = \tau^{-1} \circ J \circ \tau が \tau によらない。「行って複素共役して帰ってくる」によって複素共役が定義できる
    • (ii)(b) J が K 上の非自明な自己同型となる
    • ようするに複素共役がちゃんと入るような体のこと
  • J体：
    • CM体 K の J による固定体 K^{+} = K^J のこと
    • (ii)(a) を満たす体のこと（CM体も含めて J 体と呼ぶ）
  • J 体と CM体の基本的な性質をおさえた
  • 例：
    • 円分体 \mathbb{Q}(\mu_m) = \mathbb{Q}(\zeta_m) は CM 体
    • \mathbb{Q}(\zeta_m + \zeta_m^{-1}) は総実な J 体で上の指数２の部分体
    • 複素共役は円分体のガロア群の中心に入るので、円分体の勝手な中間体はJ体
    • さらにクロネッカー・ウェーバーより、Q上のアーベルな代数体はすべてJ体（思った以上に広い！）
    • Q上アーベルでないCM体やQ上ガロワではないCM体もたくさんある

2/18：イデアル類群の構造の補足（3.1.3）（つづき）

  • ヒルベルトの定理90が出てきた（CM体に限らず成り立つ）
    • ノルムが 1 の勝手な単元 \zeta \in \mu_{K_{n+1}^{{\rm cyc}}} に対して a\in K_{n+1}^{{\rm cyc}} が存在して \zeta = \zeta'^{g-1} と表せる
    • 群コホモロジーの言葉で表すと H^1 \left(K_{n+1}^{{\rm cyc}} / K_{n}^{{\rm cyc}}, \mu_{K_{n+1}^{{\rm cyc}}} \right) = 1
  • CM体 K のイデアル類群の構造について学んだ
    • A_n = {\rm Cl}(K_n^{{\rm cyc}})[p^\infty] とおく．このとき i_{n, {n+1}} \colon A_{n}^{-} \to A_{n+1}^{-} は単射． A_n^{-} は K の複素共役が -1 倍で作用する A_n の部分群
    • \newcommand{\lcyc}{\Lambda_{{\rm cyc}, K}} \lcyc = \mathbb{Z}_p[[\Gamma_{{\rm cyc}, K}]] とおく． \newcommand{\x}{X_{K_\infty^{{\rm cyc}}}} \x は複素共役 J の作用の固有分解によって \x = \x^{+} \oplus \x^{-} とかける（これがよく見る分解か！）
    • \lcyc 加群 \x について：
      • \x^{-} は非自明な擬零部分 \lcyc 加群を持たない
      • \x^{+} は擬零 \lcyc 加群と思われている．一般には自明ではない（らしい）

2/19：イデアル類群に関して知られた結果や予想（3.1.4）

  • 「代数体 K 」と「有限体 \mathbb{F}_q 上の１変数代数函数体 K」の類似の哲学
    • 「イデアル類群 {\rm Cl}(K)」と「代数曲線 C = C_K/\mathbb{F}_q の因子類群 {\rm Cl}_C(\mathbb{F}_q)」
    • {\rm Cl}_C(\mathbb{F}_q) \simeq {\rm Cl}_C(\overline{\mathbb{F}_q}) \simeq (\mathbb{Z}/l\mathbb{Z})^{\oplus 2g}
      • 因子類群はテイトモジュールとかいうやつかしら？（よくわかっていない）
    • 因子類群に対して類数公式の類似 {\rm Cl}(k_n)[l^{\infty}] = l^{2gn + v} が成り立つ。
      • 位相的生成元をフロベニウスに置き換えればそのまま証明できる
    • 函数体では \mu = 0 となり \mu 不変量は現れない
    • 函数体では定数体があり、代数体にはそれがないので単純には比較できない
    • 一方で、函数体における定数体の \mathbb{Z}_l 拡大を「１のベキ根を加える拡大」と捉え直すと、代数体 K の円分 \mathbb{Z}_p 拡大が「正当な」類似とみなせる
  • 以上の類似の哲学により、以下の予想が得られる（岩澤）
    • K を勝手な有限次代数体。このとき円分 \mathbb{Z}_p拡大 K_{\infty}^{{\rm cyc}}/K に対して \mu(K_{\infty}^{{\rm cyc}}) = 0 となる
    • これが \mu = 0 予想か！！！
    • 適当ではなくて、上のようなちゃんとした類似の根拠があった上での予想だったのですね（岩澤先生すごい）
  • 一方で \mu をいくらでも大きくできる円分でない \mathbb{Z}_p拡大も岩澤先生が構成している
    • 反円分 \mathbb{Z}_p拡大 K_{\infty}^{{\rm ac}}（拡大が二面体群になる）
    • これとの合成体をとると、種の理論（まじで！？） により得られる

2/20：イデアル類群に関して知られた結果や予想（3.14）（つづき）

  • \mu = 0 予想の「証明済み」な最も強い結果：Ferrero-Washington
    • K が \mathbb{Q} の有限次アーベル拡大であるとき \mu(K_{\infty}^{{\rm cyc}}) = 0 が成り立つ
  • Riemann-Hurwitz の公式
    • 「代数体のイデアル類群から定まる \lambda不変量」と「正標数の函数体のモデルである代数曲線の種数」の間の類似
    • (-) 部分の \lambda 不変量の変化を記述する

2/21：p進L函数（3.2）

  • （昨日の続き）Riemann-Hurwitz の公式
    • 木田による証明 [66] は，種の理論によって直接 \newcommand{\cyc}{{\rm cyc}} \#{\rm Cl}(K_n^{\cyc})^{-}[p^{\infty}] と \#{\rm Cl}(K_n^{\cyc})^{-}[p^{\infty}] の違いを計算する方法
    • 岩澤 [56] によって \newcommand{\gal}{{\rm Gal}} \gal (K{'}_{\infty}^{\cyc}/K_{\infty}^{\cyc} ) 上の加群 X_{K_\infty^{{\rm cyc}}}^{-} を有限群の線形表現の手法で調べる別証明
    • K, K' がアーベル体のときは，岩澤種予想を介して「p進L函数に対する木田の公式」として翻訳される
  • （昨日の続き）函数体における類似が見当たらない予想もある
    • Vandiver予想： K = \mathbb{Q}(\zeta_p)^{+} のとき X_{K_\infty^{{\rm cyc}}} = 0
    • Greenberg予想：総実代数体の円分 \newcommand{\zp}{\mathbb{Z}_p}\zp拡大において \lambda = \mu = 0（ X_{K_\infty}^{{\rm cyc}} は有限）
  • ここからp進L函数のお話（やっときたぜ！）
  • ２通りの方法でp進L函数（Thm 3.29）を構成する
    • Stickelberger元を用いた岩澤構成
    • 円単数を用いたColeman構成
  • まず，Dirichlet指標を定義した

2/22：解析的p進L函数の存在定理（3.2.1）

  • Dirichlet 指標の積を定義した
    • 異なる指標を持つ原始的ディリクレ指標 \eta, \eta' をそれぞれ誘導して等しい法を持つディリクレ指標とみなして、素朴に積をとる
    • さらにその積に付随した原始的なディリクレ指標を \eta \eta' とする
    • このときすべての原始的なディリクレ指標全体に自然なアーベル群の構造が入る
  • 原始的なディリクレ指標に対しDirichletのL函数を定義する（実際は原始的でなくてもいいが、原始的なオイラー積からオイラー因子を抜いただけのものになる）
    • L函数は複素平面全体で解析接続する
    • 負の整数点で代数的整数となる
  • p進L函数の存在定理
    • 岩澤代数 \Lambda_{\cyc, \psi} \simeq \zp[\psi][[T]] の元で以下の性質を満たすp進L函数 L_p(\psi) が存在する（ \psi = \mathbf{1} のときは \frac{1}{\gamma - \kappa_{\cyc}(\gamma)} \Lambda_{\cyc, \psi} の元）
    • p進L函数 L_p(\psi) は，L函数の負の整数点を補間してできる（ \psi は導手が Np^e（ e=0, 1）で \psi(-1) = 1 なる原始的なディリクレ指標）

2/23：解析的p進L函数の存在定理（3.2.1）（つづき）

  • \Lambda_{\cyc, \psi} \to \zp[\psi] と \Lambda_{\cyc, \psi} \to \zp[\psi] [[T]] \to \zp[\psi] は可換
  • としておいて A(T) \in \zp[\psi][[T]] をとる． r \equiv r' \pmod{p^n} とすると， A(T)\big|_{T=(1+p)^r - 1} \equiv A(T)\big|_{T=(1+p)^{r'} - 1} \pmod{p^{n+1}}
    • これは「クンマーの合同式」ですね！！！
    • A(T) の級数展開と T = (1+p)^r - 1 の二項展開の計算からただちにわかる（→やってみよう！！！）
    • A((1+p)^{r} -1) = \left(1 - \frac{(\psi \omega^{-r})(p)}{p^{1-r}}\right)L(\psi \omega^{-r}, 1-r) とするとまさにクンマーの合同式（→これも確かめよう！！！）
  • 久保田-Leopoldt は s\in \mathbb{C}_p の部分領域上の解析函数として定義したが，この本では岩澤代数の元として定義する（このほうが主予想の定式化としても便利だし、久保田-Leopoldtが導けるなど（逆は成り立たない）強い性質を持つ）
  • \psi = \mathbf{1} のときは， (\gamma - \kappa_{\cyc}(\gamma)) L_p(\mathbf{1}) \in \Lambda_{\cyc}^{\times} 可逆元となることが容易に示せる

雑感

  • ついにp進L函数きたーーー！！！
  • クンマーの合同式も出てきたし、やっと知りたかったことに近づいてきた感じがある（泣きそう）
  • 代数パートの議論で、岩澤代数を形式的べき級数環として環論的に考えるやり方に慣れてきたので、ずいぶん理解がスムーズになっていると感じる。L函数が岩澤代数の元だと言われても動揺しない。長い道のりだったけど、ちゃんと途中を飛ばさないで丁寧に進んできて良かったと感じた
  • クンマーの合同式の証明が，多項式環の単なる計算問題となってしまうのは驚き
    • 「L函数の整点をp進補間する岩澤代数の元が存在する」という存在定理があれば，クンマーの合同式は半自動で導かれるのですね！
      • 一般に，岩澤代数の形式的べき級数の性質から，級数の値の間の合同関係が導かれる
      • それぞれの値には，L函数の整点の値が割り当てられている
      • L函数の整点の間には、合同関係が成り立つ
    • 存在定理すげえな！あとで絶対に確認しよう
  • 一方で，p進L函数の「実態」がまだ掴み切れていないので、もう少し自分で計算してなれる必要がありそう。そもそも指標があんまりよくわかっていないのでそのあたりから。
  • 肝心の進捗状況だが、若干予定よりペースが遅いと考えている（計画より12, 3ページ遅い）。このままのペースだと３月末で120pとなり、岩澤主予想まで終わらない
  • 最近少しずつ朝に起きれなくなりつつあるので、もう少し気合を入れ直さないと

f:id:tsujimotter:20170223093312p:plain:w400
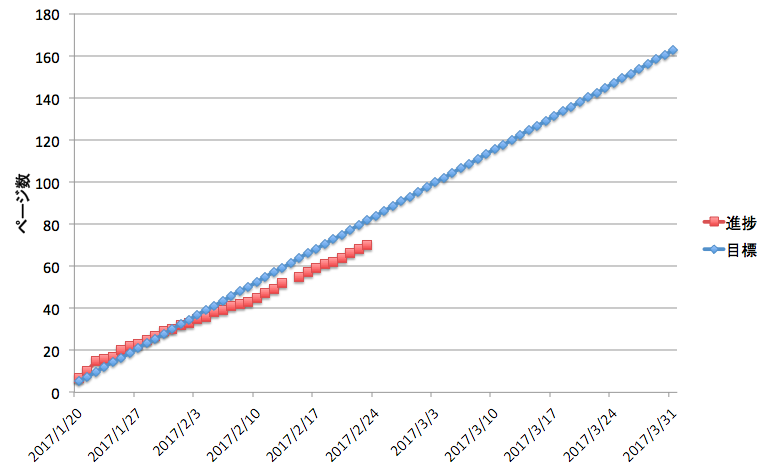
現在の進捗状況と目標ページ数の比較