tsujimotter-sub.hatenablog.com
の第7週目(なかなかしんどい週だった)。
ポイントをまとめていく。あくまで自分のメモ用です。
第7週目(2017/3/3 〜 3/9)
3/3:Coleman写像によるp進L函数の構成(3.2.4)(つづき)
- (あとで全体像を理解してから書いているメモ)
加群
の自己準同型写像
を
で定義した。
- これはあとでわかるが単なる微分を考えている。
を代入して変数変換すると,
となる
- これはあとでわかるが単なる微分を考えている。
によって定まる
の完全列を示した
3/4:Coleman写像によるp進L函数の構成(3.2.4)(つづき)
あとでまとめる
3/5:Coleman写像によるp進L函数の構成(3.2.4)(つづき)
あとでまとめる
3/6:Coleman写像によるp進L函数の構成(3.2.4)(つづき)
- ノルム系から
への写像(Coleman写像の合成写像)の完全系列を作った(Thm3.54)。
- 以上の写像の像の元として Stickelberger 元を定義した
- Stickelberger元に指標を適用して,ガウス和をかけたものを考えた
- 次回からp進L函数の別構成がはじまるらしい
3/7:Coleman写像によるp進L函数の構成(3.2.4)(つづき)
- ようやくp進L函数の構成ができた
に関係するのは補題3.55か
はノルム系(補題3.46で具体例を与えたもの)
3/8:Coleman写像によるp進L函数の構成(3.2.4)(つづき)
- これまでの構成の手順をまとめた
- (A) 円単数のノルム系
Colemanべき級数
の元
- (B)
の対数微分が
の特殊値の母函数
と「ほぼ等しい」
- (A) 円単数のノルム系
の箇所を省いてもp進L函数の新しい構成はできるが、
のステップを挟むことで、p進L函数と円単数が結びつき、岩澤主予想の円単数のEuler系を用いた証明に使えるらしい。
- わからない点:
- 「対数微分」「母函数」と言っている部分はどこのことを指しているのだろう
- 『
の対数微分が
の特殊値の母函数
と「ほぼ等しい」
が 3.2.2 項ですでに直接構成されている』らしいのだが、それはいったいどの話であろうか
- あ、わかったかも!!!
- Ferrero-Washingtonの定理(
の
不変量は自明)とLeopoldtの公式(
のp進L函数の特殊値は、p進対数関数によってかける)に触れた
3/9:代数的側面と解析的側面の関係(岩澤主予想)
- 円分岩澤主予想の定式化を行った.
- ついに岩澤主予想だ!!!うおおおおお!!!
- 円分岩澤主予想の定式化:
- Dirichlet指標を
の有限次アーベル拡大のガロワ群の指標とする.
を
に対応する体とし,
を
の円分
拡大とする.
- 二種類の不分岐拡大を定義:
を「到る所不分岐かつアーベルな最大pro-
拡大」とする
を「
の外で不分岐かつアーベルな最大pro-
拡大」とする(こっちのほうがでかい拡大)
- 対応するガロア群を定義する:
(こっちはねじれ
加群)
(こっちはねじれ
加群ではない)
版岩澤主予想
を導手が
の
であるDirichlet指標とすると以下が成り立つ
- Dirichlet指標を
-
版は次回(
がねじれ加群とは限らないので,ポントリャーギン双対をとらないといけない?)
雑感
- ようやくColeman写像によるp進L函数の構成がおわった。正確にいうと「終わらせた」という感じに近くて、証明の流れはほとんどよくわかっていない。
- 記号が難しくて飲み込みづらかったのと、構成までの過程が長くて全体像をつかむのが難しかった。全体像は最後の説明で、多少はわかった気がしないでもないので、もう一度 3.2.4 の最初から見直した方が良さそう。。。
雑感2(3/9)
- と思っていたら急にわかってきたのでまとめなおしてみる!
の特殊値(すなわち,ベルヌーイ数
)の母函数
とは 3.2.2 で次のように定義されていた;
- ここから
を取り出すには,
回微分して
をとればいい。
- ここから
- さて,ここで
と定義されており(対数をとっただけ),この
に
を
回作用させる。
は
とすると実質的に
と同じになる。
のとき
であったことを思い出そう(
のわかりやすい有理函数の形になっている)
- これがコールマン写像であることを確認するには,
に
を代入してみれば良い。
となって,ノルム系の数列が取り出せる(すなわち,
は
の母函数になっていたのだ)。
- ここで,
に数論的指標
を適用して計算していく
とすると,
にそっくりな項を
で
回微分する形の式がでてくる。
回微分して
とすると、
が飛び出す!という流れだ
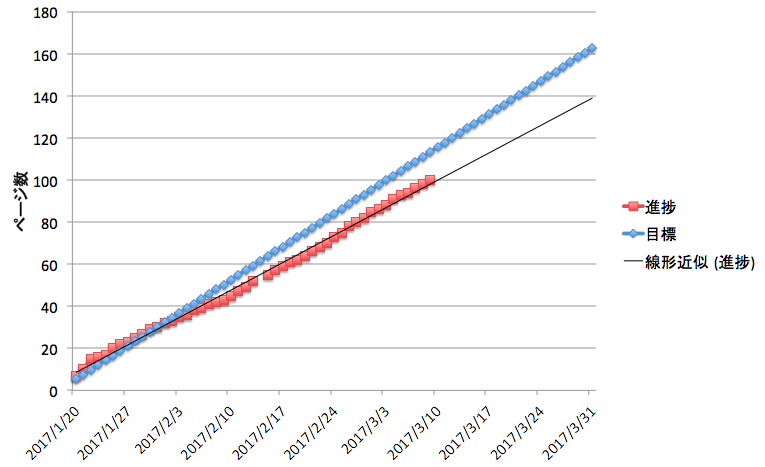
現在の進捗状況と目標ページ数の比較
とにかく止めないで先に進むことを念頭に入れて進めたので、今回の節のペースは若干早かった。おかげで少しペースを取り戻しつつある。