tsujimotter-sub.hatenablog.com
の第10週目。
ポイントをまとめていく。あくまで自分のメモ用です。
第10週目(2017/3/24 〜 2017/3/31)
3/24:WilesによるIMCの証明 (Step I)
- 基本的な方針はRibetの定理の議論の一般化
- ところどころにそのままではうまくいかない箇所が存在して、それを切り抜ける方法が鮮やかで面白い。Wilesさんすごい!
- Eisenstein級数のp進族
進モジュラー形式
を考える.
はp進L函数
で
が与えられる(これがp進Eisenstein級数?)
は
のq展開によっても与えられる。このような構成はp-安定化と呼ぶらしい。
- p安定化では、p以外のすべてのHecke作用その固有多項式は変わらない
- 方針
- 解析的類数公式があるので,
を含む高さ1の素イデアル
に対して,p進L函数の
に対する
が,
以下であることを示せばよい(p進L函数の作るイデアルが特性イデアルに含まれる(Ribetと同じ状況))
不変量の消滅定理より,上記の
はpの上にない素イデアル(
成分はない)ので、
の標数は0としてよい
をp進L函数を
が割り切る回数としておく
- 解析的類数公式があるので,
(StepI)
上の有限平坦な局所整数
,Hecke固有カスプ形式
と
の上にある
の素イデアル
が存在して,
- Ribetの議論(Step1)を追って実行するが、ところどころやり方が異なる
- Ribetでは類数の漸近評価を駆使して「定数項が単数となるモジュラー形式」を見つけたが、一般のNeben指標に対して、
進モジュラー形式の空間の次元は導手に応じて大きくなってしまう。現実的に不可能
- Wilesはこの議論を避けて「
が
と共通の零点を持たないモジュラー形式」をみつける議論で切り抜けた
- Ribetではモジュラー形式の空間を「カスプ形式の空間」と「Eisenstein級数の空間」に分けたが、今回の場合は後者の階数が高いためそのままでは難しい
- WilesはHecke作用素の作用も取り入れてうまく空間の階数の大きさを処理した。これによって正規化された
進カスプ形式
を得る(Step I終わり)
- Ribetでは類数の漸近評価を駆使して「定数項が単数となるモジュラー形式」を見つけたが、一般のNeben指標に対して、
3/25:WilesによるIMCの証明 (Step II)〜(StepIV)(完成!)
あとで書く
3/26:Euler系の方法による証明(3.3.3)
- 今日から,Euler系を使ったIMCの証明に入る。
- Thaine のアイデアを経て Kolyvagin によって発見された
- 岩澤基本完全列*1という大事な完全列について
- 類体論により
次について完全列が得られる。左の単射はLeopoldt予想により(
が
または虚二次体の有限次アーベル拡大の場合正しい)
- 4項が副有限群なのでMittag-Leffler条件が満たされ逆極限をとっても完全列になるらしい
- (単数のなす)Euler系
について:
- ノルム
をとると
が
となり,
- ノルム
をとると
が
となる(
-オイラー因子がかかる)
- ような系のことをEuler系という。
- ノルム
- このような都合のよいものが存在すれば、IMCが証明できるらしい(明日示す)。存在することは全然自明ではないが、実はこのあいだのノルム系の例をちょっと変形するとEuler系が構成できるのだ!(面倒なので書かない)
- Euler系は上の完全系列のたぶん一番左側の元になるので、Coleman写像でp進L函数を作ると、完全列の中でIMCが示せるのかなと勝手に考えている
3/27:Euler系の方法による証明(3.3.3)
- Rubin と Greither によって示された定理3.80を仮定すると「(+) 版岩澤主予想」が導けることを確認した.
- かなり複雑で込み入っていたので,図でまとめてみた

3/28:Euler系の方法による証明(3.3.3)(つづき)
- 定理3.80の証明のための道具を準備した
- セッティングについて:
の定義が疑問だったのだが,要するに
と分解したときに「
はすべて指数が1」で「
と互いに素な奇素数」を考えたいのだということがわかった.あとで,Kolyvagin作用素の定義で,
を素因数分解する
- たしか,イントロの章で「Euler系では
のような元を考えたい」みたいなことを言っていたが,こういうことだったのか.
という仮定をおく「
の勝手な素因数
に対して,
の素イデアル
は,拡大
で完全分解する」
より(円分拡大の定義を思い出そう)
が仮定を満たすなら,円分体
で
が完全分解するので,円分体の類体論より
が成り立つ
- Kolyvagin作用素とKolyvagin積分
という同型がある(
で
が総実代数体なので
となる.Inf-Res完全系列をみれば制限写像が同型になる)
- Kolyvagin作用素
はガロア群を
について分解したものを,変な感じで組み合わせて定義する.
- 帰納法を使って上記の同型の右辺側の元であることがわかる(ガロア群によって固定される)
- Kolyvagin積分は上記の元を同型の左側に引き戻す作用(というかその作用で得られた元)
- 「積分」という感じはあまりしない
- Kolyvagin作用素
3/29:Euler系の方法による証明(3.3.3)(つづき)
- 定理3.80の証明のための道具の準備段階だが,分からないゾーンに来てしまったかもしれない
- Prop. 3.87(Euler系のノルム性質とKolyvagin作用素の性質から), Prop. 3.88(Chebotarevの密度定理から) が重要な役割を果たすらしい
3/30:Euler系の方法による証明(3.3.3)(つづき)
- 岩澤加群の構造定理などを使って,Rubinの不等式を基本的な
に帰着した
- 左辺がイデアル類群
の特性イデアル(的なもの)
- 右辺が Euler 系(大域的な単数群)の極限(p進L函数的なもの)の作る単項イデアル(
倍)
- 左辺がイデアル類群
- この状況の下で,イデアル類群と大域的な単数群を
次の中間体の変動に関してコントロールする
- それぞれのKer, Cokerを零化するイデアル
を用意している?
- それぞれのKer, Cokerを零化するイデアル
3/31:Euler系を用いた方法による証明(3.3.3)
- 今までの道具を使って Rubin の不等式
を証明する流れをおった。ざっくり流れを説明
- 第n次中間体での素イデアル
の持ち上げ
をガロア作用に配慮しつつ選ぶ。Chevotarev の密度定理により、このような持ち上げは無数に存在する
- Euler系を使って,このような
を数珠つなぎ的につなげていくと
が
を割り切ることを示せる
- 第n次中間体での素イデアル
- 長かったけど、これにて Euler系 を用いた方法による証明おわり。
- 「ガロア作用に配慮した素イデアルの持ち上げ」を見つけるような複雑な箇所は「ガロア変形によるEuler系の理論」を導入することで気にしなくてよくなるらしい。これについては下巻8章で登場するらしい。
雑感
- 前半はWilesによる「モジュラー的な手法を用いた岩澤主予想の証明」後半はRubinによる「Euler系を用いた岩澤主予想の証明」を追った。
- (少し感想を書く)
- これにて 141ページが終わりました。当初の目標では「3/31までに岩澤理論とその展望(上)の本文パート162ページを終わらせる」ということだったのですが、2月終了時点ごろに「やばい、終わらない」と気づきました。そのあたりから「ひとまず3月中に岩澤主予想の2つの手法(モジュラー・Euler系)を理解しよう」と目標を下方修正していました。岩澤理論の根幹は「岩澤類数公式」「p進L函数」「岩澤主予想」の3つなので、これらの3つについて主要な証明法を理解できれば、最初の3ヶ月の目標としては十分だと考えたからです。実際、この目標はなんとか3/31までに達成することができました。進捗の状況は以下の通り。
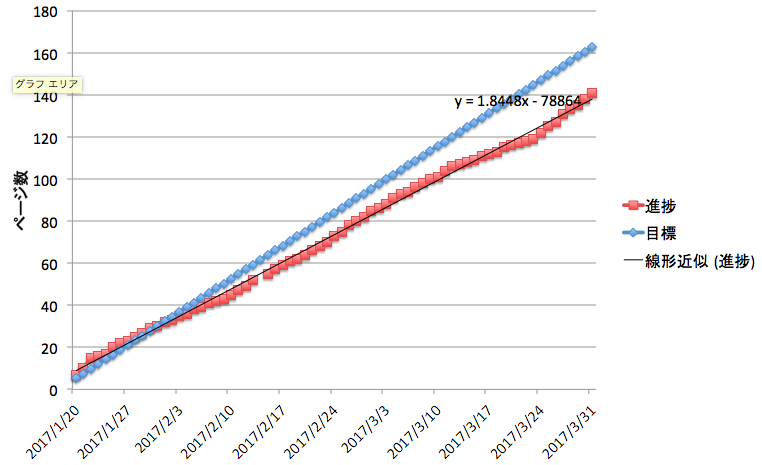
- 近似曲線を見る限り、1日1.84ページとなっていますから、(当初の目標ほどではないものの)なかなかのハイペースでここまでこれたと思います。途中、難しいパートに入ったり(Euler系とか)気持ちが落ち込んで、ペースにムラが出てきていますが、なんとかやってこれて良かったです。
- 残りの20ページに関しては、ほかの基礎体における岩澤理論と下巻への展望で構成されています。これも4月のできるだけ早い時期に完了したいと考えています。
- あとで続きを書く
*1:と呼んでいるひとがいた