メモ：線形空間の基底と普遍性、そして随伴

結城先生のツイートと黒木玄さんのツイートをきっかけに、下の記事の命題2.13が圏論的に解釈できることを理解した。
tsujimotter.hatenablog.com

できれば本ブログでもまとめたい感じの内容ではあるけど、メモがてらこちらのブログに書いておく。

集合を対象とし、その間の写像を射とする圏 $\newcommand{\sets}{{\bf Sets}} \sets$
体 $K$ 上の有限次元 $K$ -線形空間を対象とし、 $K$ -線形写像を射とする圏 $\newcommand{\vec}{{\bf FDVec}} \vec_K$

の二つの圏を考える。また、線形構造を忘れる忘却関手 $U\colon \vec_K \to \sets$ を考える。

ここで、ベクトル空間 $V, W \in \vec_K$ を考えて、 $V$ の基底 $X = \{x_1, \ldots, x_n \}$ を考えると、 $X$ は $U(V)$ に埋め込まれていると考えられるので、 $\iota \colon X \to U(V)$ なる $\sets$ の射があると思うことができる。

基底の行き先を与えるルールは、 $X$ から $U(W)$ への $\sets$ の射だと思うことができる。

というわけで、こんな感じの主張と図式に置き換えることができる。

f:id:tsujimotter:20210128114103j:plain:w600

すなわち、 $\sets$ の射 $\phi\colon X \to U(W)$ に対して、 $\vec_K$ の射 $f\colon V \to W$ が一意的に定まるわけだ。こういう構造を一般に普遍性というらしい。

今まで普遍性の例として、「直積」とか「準同型定理」みたいな構造しか知らなかった。つまり、一つの圏で完結するものしか知らなかったのですが、本当は関手があって二つの圏をまたいでいる構造なのですね。上の構造で二つの圏が同じ圏であるものを想定して、 $U$ として恒等関手を考えれば、よく知っているやつになりそう。こういう一般化は知らなかったので、とても新鮮でした。（単に不勉強で定義をよく知らなかったという話ですが。）

続いて、自由生成関手（名前はちゃんと知らないので適当） $F\colon \sets \to \vec_K$ を用意する。これは忘却関手 $U$ の逆方向の関手である。集合 $X$ を基底とするような自由 $K$ -ベクトル空間を考えることができる。つまり

$F(X) := K x_1 + K x_2 + \cdots K x_n$

というわけだ。これは $\vec_K$ の対象である。これを自由生成関手 $F$ の定義とする。

このとき、先程の $V$ を $F(X)$ に置き換えてやるとこういう図式が得られる：

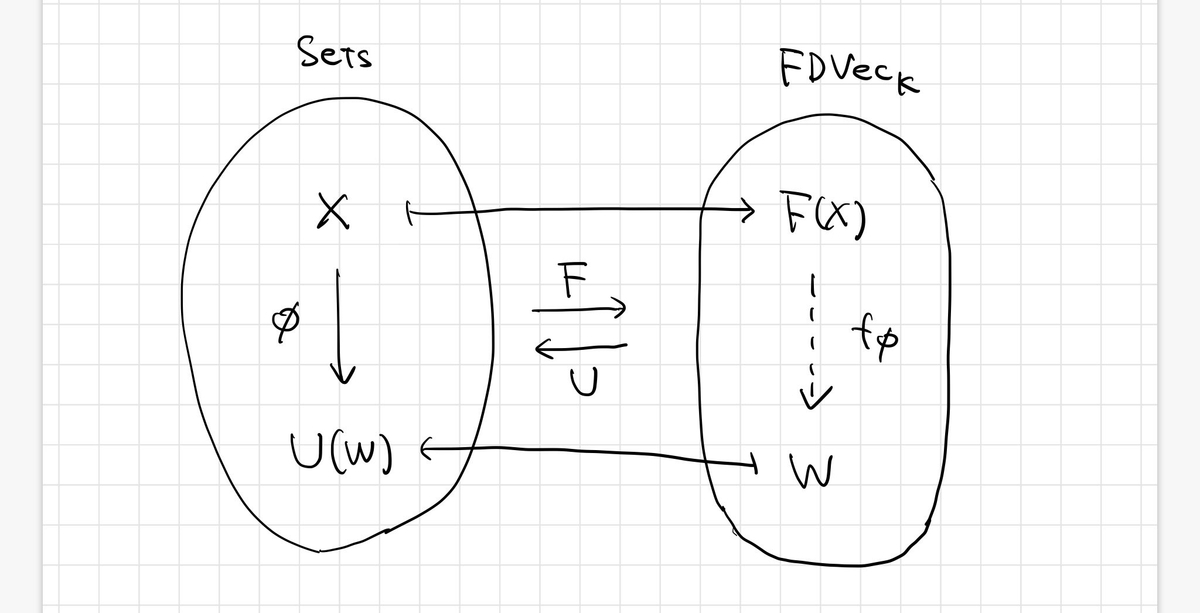
f:id:tsujimotter:20210128115104j:plain:w600

普遍性により、 $\sets$ の射 $\phi \colon X \to U(W)$ に対して、一意的に $\vec_K$ の射 $f_\phi \colon F(X) \to W$ が定まるわけだが、これが以下の自然同型に繋がるらしい。

$\operatorname{Hom}_{\sets}(X, U(W)) \simeq \operatorname{Hom}_{\vec_K}(F(X), W)$

自然同型の定義がよく分かっていないが、とりあえず一対一対応があるのはわかる。

そして、こういう関係こそ、まさに随伴という構造になっている。関手 $F, U$ は随伴の関係にあるとか、 $F$ は $U$ の左随伴関手だとか、そういう言い方をするらしい。

ついでにいうと、 $F$ が $U$ の左随伴関手だとすると、 $U \circ F$ をモナドというらしい。今回の場合だと、基底 $X$ から生成する自由ベクトル空間 $F(X)$ をとって、その線形性を忘れた集合を $U(F(X))$ としたとき、 $X$ に対して $U(F(X))$ を与える関手 $T = U \circ F$ がモナドということになる。だから何だという感じがするが、そういうものがとにかく定義されるらしい。